Giống như QuickSort , Merge Sort là một thuật toán Chia và Trị.
Bài Toán
Cần sắp xếp mảng A[1...n]. Thuật toán sắp xếp trộn được phát triển dựa trên chia để trị, bao gồm các thao tác sau:
- Chia (Divide):
- Chia dãy gồm n phần tử cần sắp xếp ra thành hai dãy, mỗi dãy có n/2 phần tử.
- Trị (Conquer):
- Sắp xếp mỗi dãy con một cách để quy sử dụng sắp xếp trộn.
- khi dãy chỉ còn một phần tử thì trả lại phần tử này.
- Tổ hợp (Combine):
- Trộn (Merge) hai dãy-con-đã-được-sắp-xếp để thu được dãy được sắp xếp gồm tất cả các phần tử của cả hai dãy con.
Nó chia mảng đầu vào thành hai nửa, gọi chính nó cho hai nửa và sau đó hợp nhất hai nửa đã được sắp xếp. Hàm merge () được sử dụng để hợp nhất hai nửa. Hợp nhất (arr, l, m, r) là một quá trình khóa giả định rằng arr [l..m] và arr [m + 1..r] được sắp xếp và hợp nhất hai mảng con đã sắp xếp thành một.
Tìm điểm giữa để chia mảng thành hai nửa:
giữa m = l + (rl) / 2. Hợp nhất phần Sắp xếp cho nửa đầu:
Call mergeSort (arr, l, m). Hợp nhất phần Sắp xếp cho nửa sau:
Call mergeSort (arr, m + 1, r). Hợp nhất hai nửa được sắp xếp ở bước 2 và 3:
Hợp nhất gọi hàm Mergesort (arr, l, m, r)
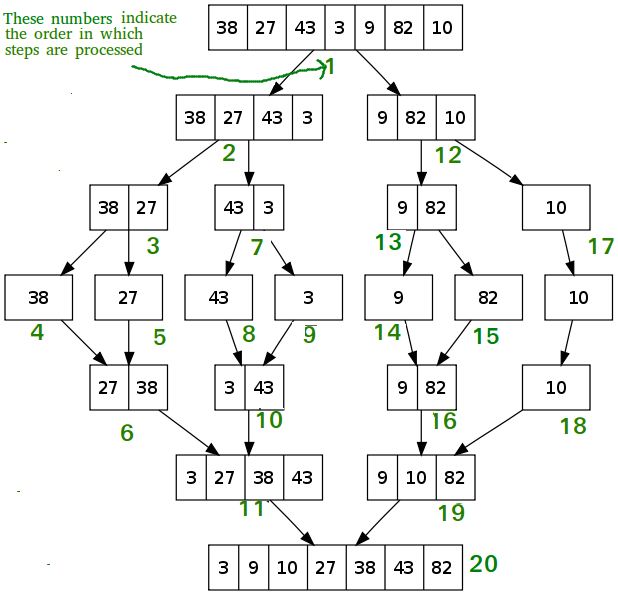
Sơ đồ sau đây từ wikipedia cho thấy quy trình sắp xếp hợp nhất hoàn chỉnh cho một mảng mẫu {38, 27, 43, 3, 9, 82, 10}.
Nếu chúng ta xem xét kỹ hơn sơ đồ, chúng ta có thể thấy rằng mảng được chia đệ quy thành hai nửa cho đến khi kích thước trở thành 1. Khi kích thước trở thành 1, các quy trình hợp nhất sẽ hoạt động và bắt đầu hợp nhất các mảng trở lại cho đến khi toàn bộ mảng đã hợp nhất.
Code hàm sắp xếp trộn
// Merges two subarrays of arr[].
// First subarray is arr[l..m]
// Second subarray is arr[m+1..r]
void merge(int arr[], int l, int m, int r)
{
int n1 = m - l + 1;
int n2 = r - m;
// Create temp arrays
int L[n1], R[n2];
// Copy data to temp arrays L[] and R[]
for (int i = 0; i < n1; i++)
L[i] = arr[l + i];
for (int j = 0; j < n2; j++)
R[j] = arr[m + 1 + j];
// Merge the temp arrays back into arr[l..r]
// Initial index of first subarray
int i = 0;
// Initial index of second subarray
int j = 0;
// Initial index of merged subarray
int k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
}
else {
arr[k] = R[j];
j++;
}
k++;
}
// Copy the remaining elements of
// L[], if there are any
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
// Copy the remaining elements of
// R[], if there are any
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
// l is for left index and r is
// right index of the sub-array
// of arr to be sorted */
void mergeSort(int arr[],int l,int r){
if(l>=r){
return;//returns recursively
}
int m =l+ (r-l)/2;
mergeSort(arr,l,m);
mergeSort(arr,m+1,r);
merge(arr,l,m,r);
}
Ví dụ Sắp xếp Trộn - Merge Sort
Đăng nhận xét